【LeetCode】363. Max Sum of Rectangle No Larger Than K 解題報告

發表於 更新於 分類於

363. Max Sum of Rectangle No Larger Than K / Hard

Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.

It is guaranteed that there will be a rectangle with a sum no larger than k.

Example 1:

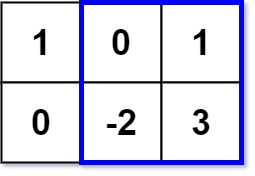
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).

Example 2:

Input: matrix = [[2,2,-1]], k = 3
Output: 3

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 100
  • -100 <= matrix[i][j] <= 100
  • -10^5 <= k <= 10^5

Solution 1: Prefix Sum on 1D Array using Sorted Container

思路

初次看到這題，心想應該就是 Prefix Sum 無誤了。以下題目大家可以參考著做，思路很像。

560. Subarray Sum Equals K
862. Shortest Subarray with Sum at Least K
1074. Number of Submatrices That Sum to Target
85. Maximal Rectangle

很像是我們把做這些題目時用到的 HashMap 尋找補數，換成用 HashSet 尋找最接近的補數。因為現在不是要找最大或特定的值，
而是要找小於 K 最接近的值。所以會用到 binary search (lower_bound) 去找補數。

效能

Complexity

  • Time Complexity: O(N^2·MlogM), where M is the height and N is the width of the matrix.
  • Space Complexity: O(M)

LeetCode Result

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& mat, int k) {
        int res = INT_MIN, m = mat.size(), n = mat[0].size();
        for (int l = 0; l < n; ++l) {
            vector<int> sums(m);
            for (int r = l; r < n; ++r) {
                for (int i = 0; i < m; ++i) 
                    sums[i] += mat[i][r];
                set<int> s = {0};
                int run_sum = 0;
                for (int sum : sums) {
                    run_sum += sum;
                    auto it = s.lower_bound(run_sum - k);
                    if (it != end(s))
                        res = max(res, run_sum - *it);
                    if(res == k) return res;
                    s.insert(run_sum);
                }
            }
        }
        return res;
    }
};

Solution 2: Improve by Kadane’s Algorithm

思路

我們可以用 Kadane’s Algorithm 做優化，關於 Kadane’s Algorithm 可以參考下面這些題
53. Maximum Subarray
918. Maximum Sum Circular Subarray

使用 Kadane’s Algorithm 可以在線性時間找出最大子陣列和的解。
我們可以想一下，剛剛我們在找 row 的和時，要用 HashSet 找補數，由於找的是補數，所以利用 Binary Search，每次多了 O(logN) 的計算。
但如果今天這個 row （Prefix Sum 的和）最大的子陣列和不超過 K，我們就可以直接更新目前的答案，而不需要去做 Binary Search。

效能

Complexity

  • Time Complexity: O(N^2·MlogM), where M is the height and N is the width of the matrix.
  • Space Complexity: O(M)

LeetCode Result

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& mat, int k) {
        int res = INT_MIN, m = mat.size(), n = mat[0].size();
        for (int l = 0; l < n; ++l) {
            vector<int> sums(m);
            for (int r = l; r < n; ++r) {
                int kadane = 0, max_kadane = INT_MIN;
                for (int i = 0; i < m; ++i) {
                    sums[i] += mat[i][r];
                    kadane = max(kadane + sums[i], sums[i]);
                    max_kadane = max(max_kadane, kadane);
                }
                
                if (max_kadane <= k) {
                    res = max(res, max_kadane);
                    continue;
                }
                
                set<int> s = {0};
                int run_sum = 0;
                for (int sum : sums) {
                    run_sum += sum;
                    auto it = s.lower_bound(run_sum - k);
                    if (it != end(s))
                        res = max(res, run_sum - *it);
                    if(res == k) return res;
                    s.insert(run_sum);
                }
            }
        }
        return res;
    }  
};