【LeetCode】1074. Number of Submatrices That Sum to Target 解題報告

發表於 更新於 分類於

1074. Number of Submatrices That Sum to Target / Hard

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

Example 1:

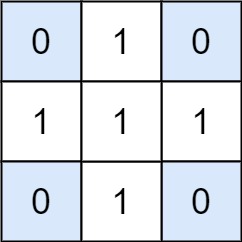
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Example 3:

Input: matrix = [[904]], target = 0
Output: 0

Comstraints

  • 1 <= matrix.length <= 100
  • 1 <= matrix[0].length <= 100
  • -1000 <= matrix[i] <= 1000
  • -10^8 <= target <= 10^8

Solution: Prefix Sum + HashMap

思路

這題最一開始只能想到暴力解，由於要暴力搜尋的是 Submatrices（子矩陣），有四個點位，
如此一來會有四層迴圈，時間複雜度高達 O(M^2 * N^2)，加上計算 Submatrice 需要 O(MN)，最後會變成 O(M^2 * N^2 * MN)。

在這裡我們要引入兩個方法來加速，一是 Prefix Sum，二是 HashMap。
在這之前，可以先看看 560. Subarray Sum Equals K 的解法，
而其解法也有 1. Two Sum 的影子。

若利用 Prefix Sum 來加速計算 Submatrice 之和，也還是會需要 O(M^2 * N^2)，這時搭配 HashMap 則可以降到 O(MN^2)。

首先我們先計算出所有 row 的 prefix sum，之後外面的兩層迴圈先決定 column 寬度，再決定要多少 row 的加總，
如果加總不是 target，就尋找上次加總減去 target 是否有存在 HashMap 中，如果沒有，就把目前的總和存進 HashMap。

效能

Complexity

  • Time Complexity: O(MN^2), where M and N are the height and width of the matrix.
  • Space Complexity: O(MN)

LeetCode Result

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
        int result = 0;
        int m = matrix.size();
        int n = matrix[0].size();
        
        // Calculate the prefix sum for every row
        for(int i = 0; i < m; ++i) 
            for(int j = 1; j < n; ++j) 
                matrix[i][j] += matrix[i][j-1];
        
        unordered_map<int, int> hmap;
        for(int i = 0; i < n; ++i) {
            for(int j = i; j < n; ++j) {
                int curSum = 0;
                hmap.clear();
                hmap[0] = 1;
                for(int k = 0; k < m; ++k) {
                    curSum += matrix[k][j] - (i > 0 ? matrix[k][i-1] : 0);
                    result += hmap.count(curSum - target) != 0 ? hmap[curSum - target] : 0;
                    hmap[curSum]++;
                }
            }
        }      
        return result;
    }
};