【LeetCode】276. Paint Fence 解題報告

發表於 分類於

276. Paint Fence / Medium

You are painting a fence of n posts with k different colors. You must paint the posts following these rules:

Every post must be painted exactly one color.
There cannot be three or more consecutive posts with the same color.
Given the two integers n and k, return the number of ways you can paint the fence.

Example 1:

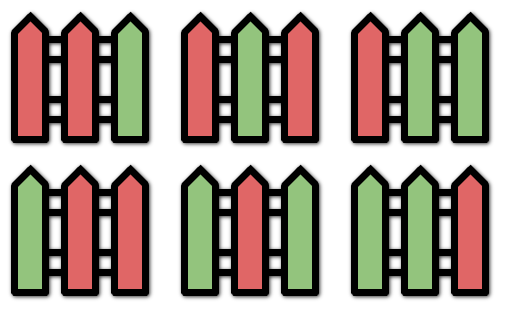
Input: n = 3, k = 2
Output: 6
Explanation: All the possibilities are shown.
Note that painting all the posts red or all the posts green is invalid because there cannot be three posts in a row with the same color.

Example 2:

Input: n = 1, k = 1
Output: 1

Example 3:

Input: n = 7, k = 2
Output: 42

Constraints:

  • 1 <= n <= 50
  • 1 <= k <= 105
  • The testcases are generated such that the answer is in the range [0, 231 - 1] for the given n and k.

Solution

思路

這種計算組合的題目，通常都需要用到 DP。要使用 DP，我們就需要確立邊界條件以及狀態轉移方程式。

以這題來說，第一塊木板會有 k 種顏色，第二塊木板會有 k^2 種顏色。我們用 ways[n] 代表 n 塊木板有幾種塗色方式。

分成兩種狀態來討論，

  1. 第 n 塊木板的顏色 和 第 n-1 塊 顏色不同
    這個情況會有 ways[n-1] * (k-1) 種組合

  2. 第 n 塊木板的顏色 和 第 n-1 塊 顏色相同
    這個情況會有 ways[n-1] * 1 種組合

因為題目有限制不能連續三塊木板同色，如果我們要 n 跟 n-1 的顏色相同，那 n-1 跟 n-2 的顏色就要不同
也就是 (ways[n-2] * k-1)

第 n 塊木板的顏色和 第 n-1 塊木板顏色不同 ways[n-1] * (k-1)
第 n-1 塊和 n-2 塊木板同色的狀況（ways[n-2] * 1 * (k-1)）

最後就會是兩者相加 ways[n] = (k-1)*(ways[n-2] + ways[n-1])

效能

Complexity

  • Time Complexity: O(N), where N is the number of the posts
  • Space Complexity: O(N)

LeetCode Result

Code

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int numWays(int n, int k) {
        vector<int> dp(n+2, 0);
        dp[0] = 1; 
        dp[1] = k; 
        dp[2] = k*k; 
        for(int i = 3; i <= n; i++) 
            dp[i] = (k-1)*(dp[i-1] + dp[i-2]); 
        return dp[n]; 
    }
};