131. Palindrome Partitioning / Medium
Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.
A palindrome string is a string that reads the same backward as forward.
Example 1:
Input: s = “aab”
Output: [[“a”,”a”,”b”],[“aa”,”b”]]
Example 2:
Input: s = “a”
Output: [[“a”]]
Constraints:
- 1 <= s.length <= 16
- s contains only lowercase English letters.
Solution 1: Backtracking
思路
用 DFS 做 backtracking,窮舉所有的可能性。
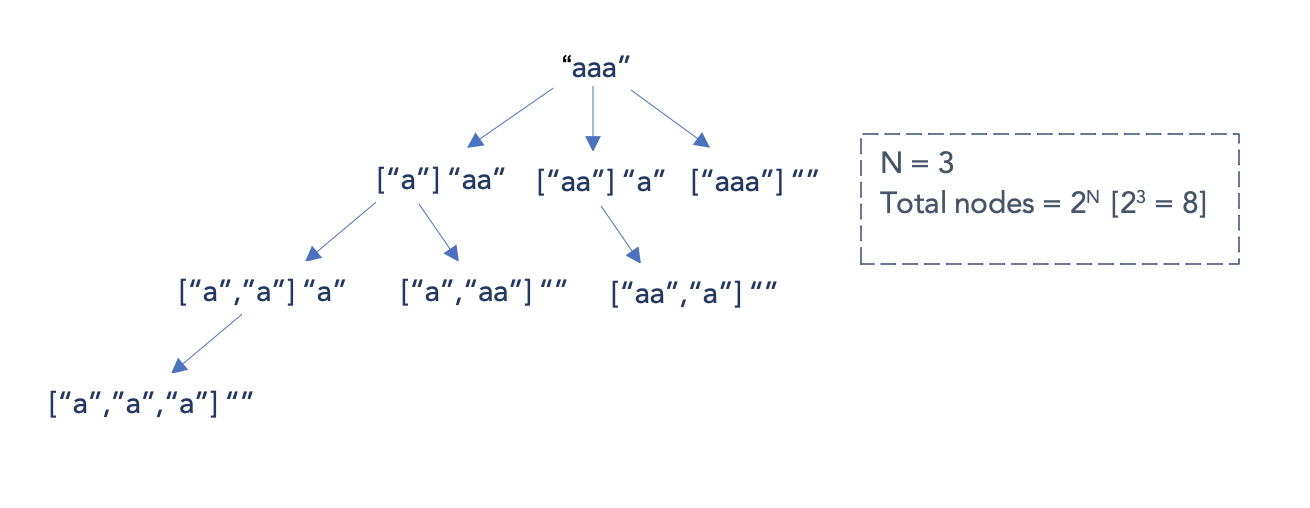
對於長度為 N 的字串來說,會展開 2^N 個節點,而每次 DFS 都需要用 O(N) 產生並判斷是否是迴文,所以時間複雜度為 O(N*2^N)
效能
Complexity
- Time Complexity: O(N*2^N)
- Space Complexity: O(N)
LeetCode Result
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public:
vector<vector<string>> partition(string s) {
vector<vector<string>> result;
vector<string> currList;
dfs(result, currList, s, 0);
return result;
}
void dfs(vector<vector<string>>& result, vector<string>& currList, string& s, int start) {
if(start >= s.size()) {
result.emplace_back(currList);
return;
}
for(int end = start; end < s.size(); ++end) {
if(isPalindrome(s, start, end)) {
currList.emplace_back(s.substr(start, end-start+1));
dfs(result, currList, s, end+1);
currList.pop_back();
}
}
}
bool isPalindrome(string& s, int l, int r) {
while(l < r) {
if(s[l++] != s[r--]) return false;
}
return true;
}
};
|
Solution 2: Backtracking + DP
思路
由於每次都要判斷是不是迴文會損失很多時間,我們利用 DP 來儲存並判斷子字串是否是迴文。
如果目前兩字元相等,而且向內(dp[start+1][end-1])是迴文,那這個字串就是迴文。
但要注意前後相減小於等於 2 的狀態,會觸及邊界。
效能
Complexity
- Time Complexity: O(N*2^N)
- Space Complexity: O(N^2)
LeetCode Result
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
vector<vector<string>> partition(string s) {
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n, false));
vector<vector<string>> result;
vector<string> currList;
dfs(result, currList, s, 0, dp);
return result;
}
void dfs(vector<vector<string>>& result, vector<string>& currList, string& s, int start, vector<vector<bool>>& dp) {
if(start >= s.size()) {
result.emplace_back(currList);
return;
}
for(int end = start; end < s.size(); ++end) {
if(s[start] == s[end] && (end - start <= 2 || dp[start+1][end-1])) {
dp[start][end] = true;
currList.emplace_back(s.substr(start, end-start+1));
dfs(result, currList, s, end+1, dp);
currList.pop_back();
}
}
}
};
|

