【LeetCode】238. Product of Array Except Self 解題報告

發表於 更新於 分類於

238. Product of Array Except Self / Medium

Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].

The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.

You must write an algorithm that runs in O(n) time and without using the division operation.

Example 1:

Input: nums = [1,2,3,4]
Output: [24,12,8,6]

Example 2:

Input: nums = [-1,1,0,-3,3]
Output: [0,0,9,0,0]

Comstraints

  • 2 <= nums.length <= 10^5
  • -30 <= nums[i] <= 30
  • The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.

Solution 1: Left and Right product lists

思路

由於暴力解會是 O(N^2)，會超時，因此我們必須善用記錄下的資料。
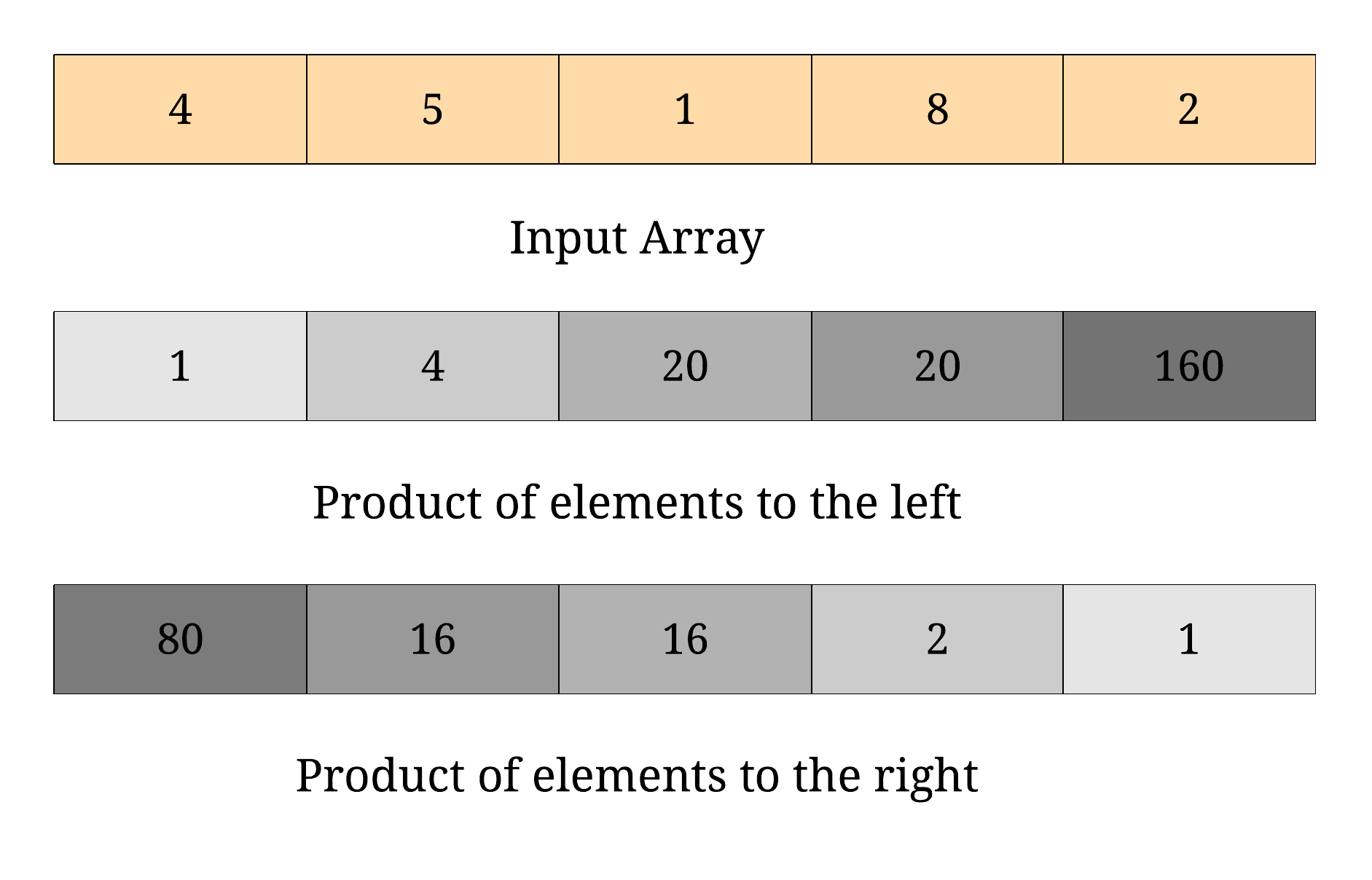
各計算出從左邊與右邊乘法的乘積陣列，然後假設要計算 i 的值，就將 p1[i-1] * p2[i+1]。
以這樣的概念，只需要掃描兩次陣列。

效能

Complexity

  • Time Complexity: O(N)
  • Space Complexity: O(N)

LeetCode Result

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        vector<int> p1;
        vector<int> p2;
        vector<int> sol;
        
        const int n = nums.size();
        
        int sum = 1;
        for(int i = 0; i < n-1; ++i) {
            sum = nums[i]*sum;
            p1.emplace_back(sum);
        }
        sum = 1;
        for(int i = n-1; i > 0; --i) {
            sum = nums[i]*sum;
            p2.emplace_back(sum);
        }
        reverse(p2.begin(), p2.end());
        
        sol.emplace_back(p2[0]);
        for(int i = 0; i < n-2; ++i) {
            sol.emplace_back(p1[i]*p2[i+1]);
        }
        sol.emplace_back(p1[n-2]);
        
        return sol;
    }
};

Solution 2: Space Complexity O(N)

思路

由於上一個思路需要另外開一個陣列，所以其空間複雜度並不為 O(N)。
首先，我們先開一個陣列，初始化為 1，將從右到左的乘積記錄下來。
接著，利用一個變數 preNum，紀錄目前從左邊的乘積是多少，一邊計算，一邊將其與原來的右乘積乘在一起，並放回陣列中。
要注意的是，不管是哪一個迴圈，都必須避開第一個值。

效能

Complexity

  • Time Complexity: O(N)
  • Space Complexity: O(1)

LeetCode Result

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        const int n = nums.size();
        vector<int> ret(n, 1);
        for(int i = n-2; i >= 0; --i) {
            ret[i] = ret[i+1] * nums[i+1];
        }
        
        int preNum = nums[0];
        for(int i = 1; i < n; ++i) {
            ret[i] *= preNum;
            preNum *= nums[i];
        }
        return ret;
    }
};